常见排序算法总结

2016-04-13
Study
Algorithm/C/Sort

一些常见的排序算法总结，为了防止自己哪天忘了可以回顾下，算法代码都用C语言来写，毕竟自己学的第一门语言。

缘起

这几个月面试了三四家公司，其中第一家

面试官：知道有哪些排序算法吗
我：嗯，冒泡，插入，选择，快排，归并，桶排
面试官：恩好，下一题
我：。。。。

如果他面试官按照常理出牌说说一下某某排序的具体思路，这就好玩了，因为有一半的我不会！！我在给自己挖坑，结果还没坑到自己。

还有一次面试

面试官：解释一下冒泡算法
我：%&￥%#……×&%%￥%￥
面试官：额。。。恩。。。。下一题。

结果证明我知道的排序算法都能解释的非常模糊，等于没讲，所以就整理一下思路，省的以后面试还是解释不清楚

为了方便说明，现在有一个数组arr，长度为n，然后按照从小到大进行排序

冒泡排序

该冒泡算法的时间复杂度是O(n2)

简单思路描述

首先arr[0]与arr[1]比较，如果arr[0]大于arr[1]则两者交换，否则不动，然后比较arr[1]与arr[2]，如果arr[1]大于arr[2]则两者交换，否则不动，以此类推，直到arr[n-1]与arr[n]比较处理完，此时最大的数就像冒泡泡那样移到arr[n]。此时第一轮循环结束，然后以此类推第二轮循环找出最大的移动arr[n-1]的位子，然后以此类推不断将最大的往后挪。

也就是说不断的访问要排序的数列，每次比较两个元素，如果这两个元素排列错误则交换过来，这样大的元素就慢慢移到后面。

图片摘自维基百科

代码

1
2
3
4
5
6
7
8
9
10
11
12
void bubble_sort(int arr[], int n) {
    int i, j, temp;
    for (i = 0; i < n-1; i++) {
        for (j = 0; j < n-i-1; j++) {
            if (arr[j] > arr[j+1]) {
                temp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = temp;
            }
        }
    }
}

选择排序

选择排序的时间复杂度和冒泡排序一样都是O(n2)

简单思路描述

首先，找到数组中最小的，并将它与第一个交换，然后找到扫一遍找到第二个最小的，并将它与第二个数交换，然后以此类推数组就排序好了

也就是说在未排序的序列中找到最小的元素，放到起始位子，然后在剩余未排序的选取最小的元素，放到排好序列的最后，这样以此类推就排好了。

图片摘自维基百科

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void selection_sort(int arr[], int n) {
    int i, j, min, temp;
    for (i = 0; i < n; i++) {
        min = i;
        for (j = i+1; j < n; j++) {
            if (arr[min] > arr[j]) {
                min = j;
            }
        }
        if (min != i) {
            temp = arr[i];
            arr[i] = arr[min];
            arr[min] = temp;
        }
    }
}

插入排序

插入排序的时间复杂度也是O(n2)

排序，插入，还有冒泡，这三种算法是我最熟悉的，因为当初大一学C语言的时候，这三种排序考试必考，不会也得会啊。当然相应的也是最简单的排序方法，所以从时间复杂度来讲也是最耗时的=。=

简单描述

首先看arr[1]与arr[0]的大小关系，将两者的顺序从小到大排序，这样从arr[0]到arr[1]是排好的，然后将arr[2]插入到arr[0]到arr[1]这序列中，使arr[0]到arr[2]是有序的序列，然后是arr[4]插入进来，以此类推就成了有序的序列。

也就是说通过构建有序序列，对于位排序的数据在已排序中进行扫描，找到相应的位子插进去。

图片摘自维基百科

代码

1
2
3
4
5
6
7
8
9
10
void insertion_sort(int arr[], int n) {
    int i, j, temp;
    for (i = 1; i < n; i++) {
        for (j = i-1; j >= 0 && arr[j] > arr[j+1]; j--) {
            temp = arr[j];
            arr[j] = arr[j+1];
            arr[j+1] = temp;
        }
    }
}

快速排序

个人感觉最重要的排序就是排序，然而现在才开始学习实在是惭愧=。=

时间复杂度为O(n*logn)，而且该算法在同为O(n*logn)的几种排序算法中效率更高。

简单描述

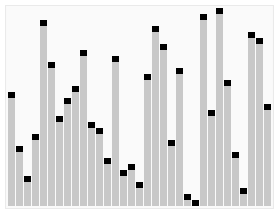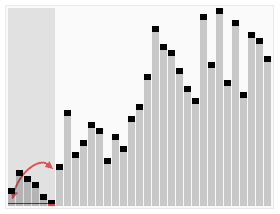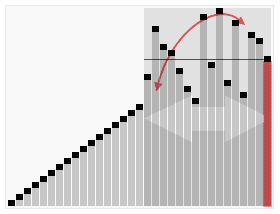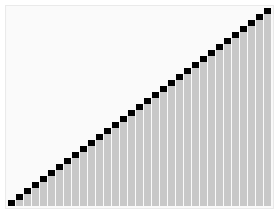
从大体上来说，该算法采用的是分治法的思想。详细步骤如下：

1、从序列中挑选出一个基准，可以是第一个，也可以是最后一个，也可以是中间的，这里以取最后一个为例。
2、重新排列序列，将比基准大的放一边，比基准小的放另一边，这样基准就处于两边的中间位子。以最后一个为基准的话，首尾指针双管齐下，首先通过首指针往后扫描找到比基准大的，然后将其移到尾指针的位置，然后尾指针往前扫描直至找到比基准小的，将其移到首指针处，如此下去直至首尾指针相遇，此时首尾指针处就是基准存放的地方。更为详细白话的介绍戳这里
3、然后对左右分区重复上述1、2操作

图片摘自维基百科

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
void quick_sort_recurse(int arr[], int start, int end) {
    int flag, left, right, i;
    if (start >= end) return;

    srand((unsigned)time(NULL));
    i = rand()%(end-start) + start;
    flag = arr[i];          //flag选取随机数，避免O(n<sup>2</sup>)的最坏情况

    /*将选取的随机数与最后一个交换*/
    i = arr[end];
    arr[end] = flag;
    flag = i;

    left = start;
    right = end;
    while (left < right) {
        while (left < right && arr[left] <= flag) {
            left++;
        }
        if (left < right) {
            arr[right] = arr[left];
            right--;
        }
        while (left < right && arr[right] >= flag) {
            right--;
        }
        if (left < right) {
            arr[left] = arr[right];
            left++;
        }
    }
    arr[left] = flag;
    quick_sort_recurse(arr, start, left-1);
    quick_sort_recurse(arr, left+1, end);
}

void quick_sort(int arr[], int n) {
   quick_sort_recurse(arr, 0, n-1);
}

归并排序

时间复杂度同样为O(n*logn)，该算法的效率也是非常不错的，只不过相比于快排，需要额外的存储空间。

简单描述

该算法也是典型的采用分治法。其思想简单的描述就是将排序好的两个序列合并成一个序列，要得到排序好的序列，就需要不断的将序列再平分，直至序列里面只有一个数字，此时序列肯定是有序的，然后再不断的合并上去，直至合并成一个有序的序列。

所以该算法的核心也就是如何有效的合并两个序列，由于序列是有序的，所以只要安排两个指向他们首部的指针，然后看两个指针指向的内容哪个小就取出来存在临时的序列中，并且指针向后移，然后接着比较两个指针指向的内容，直至某个指针指到末尾，然后另个序列的余下内容再接着补上。

图片摘自维基百科

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void merge_sort_recurse(int arr[], int temp[], int start, int end) {
    int mid, left, right, merge;
    if (start >= end) return;

    mid = (end-start) / 2 + start;
    merge_sort_recurse(arr, temp, start, mid);
    merge_sort_recurse(arr, temp, mid+1, end);
    left = merge = start;
    right = mid+1;

    while (left <= mid && right <= end)
        temp[merge++] = (arr[left] < arr[right]) ? arr[left++] : arr[right++];

    while (left <= mid)
        temp[merge++] = arr[left++];

    while (right <= end)
        temp[merge++] = arr[right++];

    for (merge = start; merge <= end; merge++)
        arr[merge] = temp[merge];
}

void merge_sort(int arr[], const int n) {
    int temp[n];
    merge_sort_recurse(arr, temp, 0, n-1);
}

碎碎念

以上则是比较常用的排序算法，祝自己找到好的实习T_T

The End~

Blog comments powered by Disqus